nrow(peng)[1] 3337 ESS Exampless
7.1 Review
Extra Sum of Squares
From last time, we basically learned what the following means:
\[ \frac{SS(\hat\beta_{q+1}, ..., \hat\beta_{p-1} | \hat\beta_0, ... \hat\beta_q)}{(p-q)s^2} =\frac{S_1 - S(\hat\beta_0) - (S_2 - S(\hat\beta_0))}{(p-q)s^2}\sim F_{p-q, \max(p, q)} \] where \(s^2\) is the MSE calculated from the larger model.
This allows us to do a test for whether \(\beta_{q+1} = \beta_{q+2} = ... = \beta_{p-1} = 0\).
Recall that this is accomplished by testing whether the variance of the line significantly changes when those predictors are included. A line with zero variance is horizontal; if adding one predictor to that line changes the variance significantly, then it’s no longer a horizontal line (and thus the slope is non-zero). This works when extending into arbitrary dimensions by adding more predictors - if a predictor is not included in a model, then the hyperplane defined by the linear regression is “horizontal” in that direction.
Mathematically, the regression equation \(y = \beta_0 + \beta_1x_1 + \beta_2x_2\) defines a plane in 3 dimensions, with the slopes determined by \(\beta_1\) and \(\beta_2\) (and a slope of \(1\) in the y direction). If we have also recorded \(x_3\) but not included it in the model, we can write the hyperplane as \(y = \beta_0 + \beta_1x_1 +\beta_2x_2 + 0x_3\), i.e. the hyperplane has a slope of 0 in the \(x_3\) direction. Adding \(x_3\) as a predictor means we are allowing the slope in the \(x_3\) direction to be non-zero.
The big lesson here is that analysing the variance allows us to determine if the slope is 0! This is very important for understanding what’s happening with regression.
Penguins Example
The R code to do this test is as follows. In this code, we believe that the bill length and bill depth are strongly correlated, and thus we cannot trust the CIs that we get from summary(lm()) (we saw “Confidence Regions” in the slides and code for L05).
lm1 <- lm(body_mass_g ~ flipper_length_mm + bill_length_mm + bill_depth_mm, data = peng)
lm2 <- lm(body_mass_g ~ flipper_length_mm, data = peng)
anova(lm2, lm1)Analysis of Variance Table
Model 1: body_mass_g ~ flipper_length_mm
Model 2: body_mass_g ~ flipper_length_mm + bill_length_mm + bill_depth_mm
Res.Df RSS Df Sum of Sq F Pr(>F)
1 331 51211963
2 329 50814912 2 397051 1.2853 0.2779Where do these values come from?
Let’s try and calculate these values ourselves in a couple different ways!
anova(lm1)Analysis of Variance Table
Response: body_mass_g
Df Sum Sq Mean Sq F value Pr(>F)
flipper_length_mm 1 164047703 164047703 1062.1232 <2e-16 ***
bill_length_mm 1 140000 140000 0.9064 0.3418
bill_depth_mm 1 257051 257051 1.6643 0.1979
Residuals 329 50814912 154453
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1From this model, SSE is 50814912 on 329 degrees of freedom. This is the same as the SSE in the output of anova(lm2, lm1).
Calculating the SSE
anova(lm2)Analysis of Variance Table
Response: body_mass_g
Df Sum Sq Mean Sq F value Pr(>F)
flipper_length_mm 1 164047703 164047703 1060.3 < 2.2e-16 ***
Residuals 331 51211963 154719
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Again, the SSE of 51211963 matches what we saw in anova(lm2, lm1), and we have 331 degrees of freedom (as expected, the differences in degrees of freedom is 2).
Note that the F-value in anova() is just the ratio of the MSEs, but this is not the case here. Instead, we need to calculate \(s^2\).
Final Calculations
\(s^2\) is the MSE for the larger model:
s2 <- 50814912 / 329
s2[1] 154452.6And now we can calculate the F-value:
(51211963 - 50814912) / (2 * s2)[1] 1.2853491 - pf(1.28539, 2, 329)[1] 0.2779278anova(lm2, lm1)Analysis of Variance Table
Model 1: body_mass_g ~ flipper_length_mm
Model 2: body_mass_g ~ flipper_length_mm + bill_length_mm + bill_depth_mm
Res.Df RSS Df Sum of Sq F Pr(>F)
1 331 51211963
2 329 50814912 2 397051 1.2853 0.2779- Try to calculate these values based on matrix multiplication.
- With and without correction factors!
7.2 ESS Algorithms
Main Idea
- ESS: Test a subset of predictors for at least one significant coefficient.
- We might want to check all predictors one-by-one.
- This is much less common than the textbook may lead you to believe
There are 3 ways to calculate the ESS for all predictors. They are very helpfully labelled Types I, II, and III.
Type I: Sequential Sum-of-Squares (with interactions)
- Check \(SS(\hat\beta_1|\hat\beta_0)\)
- Check \(SS(\hat\beta_2|\hat\beta_0, \hat\beta_1)\)
- Check \(SS(\hat\beta_2:\hat\beta_1|\hat\beta_0, \hat\beta_1, \hat\beta_2)\)
- \(\hat\beta_2:\hat\beta_1\) is an interaction term, which means we use a formula like
y ~ x1 + x2 + x1*x2(although we’ll learn why R uses different notation than this).
- \(\hat\beta_2:\hat\beta_1\) is an interaction term, which means we use a formula like
- Check \(SS(\hat\beta_3|\hat\beta_0, \hat\beta_1, \hat\beta_2)\)
- Check all interactions between x1, x2, and x3,
- …
This will give us every possible sum-of-squares. This is very very dubious, and can lead to a major multiple comparisons problem!
Type 2: Sequential Sum-of-Squares (R’s Default)
- Check \(SS(\hat\beta_1|\hat\beta_0)\)
- Check \(SS(\hat\beta_2|\hat\beta_0, \hat\beta_1)\)
- Check \(SS(\hat\beta_3|\hat\beta_0, \hat\beta_1, \hat\beta_2)\)
- …
- Results in an ordered sequence of “is it worth adding x1?”, “if we have x1, is it worth adding x2?”, etc.
- Only meaningful if the predictors are naturally ordered (such as polynomial regression, see below).
Type 3: Last-entry sum-of-squares
- Check \(SS(\hat\beta_1|\hat\beta_0, \hat\beta_2, \hat\beta_3)\)
- Check \(SS(\hat\beta_2|\hat\beta_0, \hat\beta_1, \hat\beta_3)\)
- Check \(SS(\hat\beta_3|\hat\beta_0, \hat\beta_1, \hat\beta_2)\)
- Whether adding predictor \(x_i\) is worth it, given that all other predictors are already in the model.
Back to Type 2 ANOVA (Sequental Sum-of-Squares)
By default, R does sequential sum-of-squares. This is a very important fact to know!
In Types I and II, the order of the predictors matters. In fact, you cannot make any conclusions about the significance that doesn’t make reference to this fact.
Type 2 ANOVA in R
## Try changing the order to see how the significance changes!
mylm <- lm(mpg ~ qsec + disp + wt, data = mtcars)
anova(mylm)Analysis of Variance Table
Response: mpg
Df Sum Sq Mean Sq F value Pr(>F)
qsec 1 197.39 197.39 28.276 1.165e-05 ***
disp 1 615.12 615.12 88.116 3.816e-10 ***
wt 1 118.07 118.07 16.914 0.0003104 ***
Residuals 28 195.46 6.98
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(mylm)$coef # No obvious connection to anova Estimate Std. Error t value Pr(>|t|)
(Intercept) 19.7775575655 5.93828659 3.33051585 0.0024420674
qsec 0.9266492353 0.34209668 2.70873496 0.0113897664
disp -0.0001278962 0.01056025 -0.01211109 0.9904228666
wt -5.0344097167 1.22411993 -4.11267686 0.0003104157Special Case: Polynomial Regression
\[ y_i = \beta_0 + \beta_1x_i + \beta_2x_i^2 + \beta_3x_i^3 + ... + \beta_{p-1}x_i^{p-1} + \epsilon_i \]
We only have one predictor \(x\), but we have performed non-linear transformations (HMWK: why is it important that the transformations are non-linear?).
What order of polynomial should we fit?
Polynomial Regression Data Context
- Given we have a linear model, is it worth making it quadratic?
- Given that we have a quadratic model, is it worth making it cubic?
- Given that we have a cubic model…
In the code below, I use the I() function (the I means identity) to make the polynomial model. The “formula” notation in R, y ~ x + z, has a lot of options. Including x^2, rather than I(x^2), makes R think we want to do one of the more fancy things, but the I() tells it that we want to literally square it. In the future, we’ll use a better way of doing this.
x <- runif(600, 0, 20)
y <- 2 - 3*x + 3*x^2 - 0.3*x^3 + rnorm(600, 0, 100)
plot(y ~ x)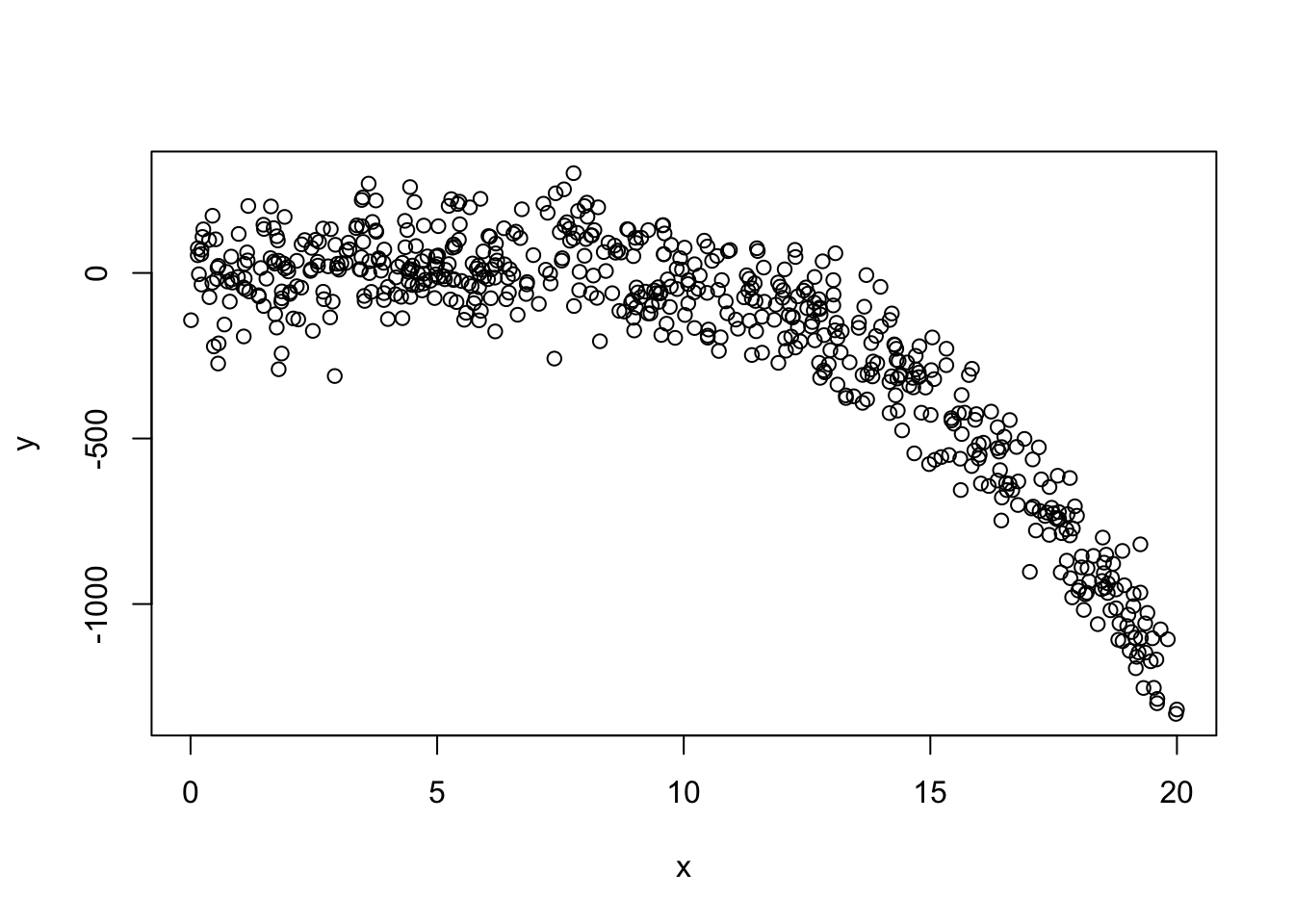
Sequential SS for Polynomial Regression
mylm <- lm(y ~ x + I(x^2) + I(x^3) + I(x^4) + I(x^5) + I(x^6))
anova(mylm)Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 49560412 49560412 4726.8201 <2e-16 ***
I(x^2) 1 19661307 19661307 1875.1955 <2e-16 ***
I(x^3) 1 1150679 1150679 109.7459 <2e-16 ***
I(x^4) 1 661 661 0.0630 0.8018
I(x^5) 1 112 112 0.0107 0.9177
I(x^6) 1 6274 6274 0.5984 0.4395
Residuals 593 6217568 10485
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1From the table above, we can clearly see that this should just be a cubic model (which is the true model that we generated). Try changing things around to see if, say, it will still detect an order 5 polynomial if if there’s no terms of order 3 or 4.
A note on calculations
Take a moment to consider the following. Suppose I checked the following two (Type II) ANOVA tables:
anova(lm(mpg ~ disp, data = mtcars))anova(lm(mpg ~ disp + wt, data = mtcars))
Both tables will have the first row labelled “disp” and include its sum-of-squares along with the F-value. Do you expect these two rows to be exactly the same?
Think about it.
Think a little more.
What values do you expect to be used in the calculation?
Which sums-of-squares? Which variances?
Let’s test it out.
Change in ANOVA when adding predictors
anova(lm(mpg ~ disp, data = mtcars))Analysis of Variance Table
Response: mpg
Df Sum Sq Mean Sq F value Pr(>F)
disp 1 808.89 808.89 76.513 9.38e-10 ***
Residuals 30 317.16 10.57
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(lm(mpg ~ disp + wt, data = mtcars))Analysis of Variance Table
Response: mpg
Df Sum Sq Mean Sq F value Pr(>F)
disp 1 808.89 808.89 95.0929 1.164e-10 ***
wt 1 70.48 70.48 8.2852 0.007431 **
Residuals 29 246.68 8.51
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1They’re different!
With both the polynomial and the disp example, we see that the interpretation of the anova table is highly, extremely, extraordinarily dependent on which predictors we choose to include AND the order in which we choose to include them. So, yeah. Be careful.
Type III SS in R
There isn’t a built-in function to do this. To create this, we can either use our math (my preferred method) or test each one individually.
anova(
lm(mpg ~ disp + wt, data = mtcars),
lm(mpg ~ disp + wt + qsec, data = mtcars)
)Analysis of Variance Table
Model 1: mpg ~ disp + wt
Model 2: mpg ~ disp + wt + qsec
Res.Df RSS Df Sum of Sq F Pr(>F)
1 29 246.68
2 28 195.46 1 51.22 7.3372 0.01139 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(
lm(mpg ~ disp + qsec, data = mtcars),
lm(mpg ~ disp + wt + qsec, data = mtcars)
)Analysis of Variance Table
Model 1: mpg ~ disp + qsec
Model 2: mpg ~ disp + wt + qsec
Res.Df RSS Df Sum of Sq F Pr(>F)
1 29 313.54
2 28 195.46 1 118.07 16.914 0.0003104 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(
lm(mpg ~ wt + qsec, data = mtcars),
lm(mpg ~ disp + wt + qsec, data = mtcars)
)Analysis of Variance Table
Model 1: mpg ~ wt + qsec
Model 2: mpg ~ disp + wt + qsec
Res.Df RSS Df Sum of Sq F Pr(>F)
1 29 195.46
2 28 195.46 1 0.0010239 1e-04 0.99047.3 Modelling Strategies
The Art of Modelling
- If you think to yourself “my predictors are logically ordered and I want to check for the significance of all of them one-by-one”, you want Type II.
- Type 1 error through the roof.
- If you think “they’re not ordered but I want to check significance”, check the overall F test for all predictors and then individual t-tests.
- If you think “what would happen if each predictor were the last one I put in the model”, then you want Type III.
- I can’t think of a good for doing this - you’re pretty much guaranteed to have a multiple comparisons issue.
Choosing Predictor Sets
- These algorithms assume that you have a set of predictors that you already know you want to check.
- There are other predictors in the mtcars dataset that we did not consider!
- We only looked at continuous predictors - we’ll see categorical predictors later.
Advice
- Start with a lot of plots.
- Based on the plots and your knowledge of the context, create a candidate set of predictors that you think will be the final model.
- Check the model fit (p-values, residuals, etc).
- Based on your knowledge of the context, check significance of groups of predictors that you think are highly correlated.
- Your final model will be based on the tests for groups of (or individual) predictors that you suspect would be relevant.
The Guiding Principles of Model Selection
Minimize the number of p-values that you check.
- ESS tests check a set of predictors, rather than each one individually.
- Fewer p-values!
- The Type I, II, and III algorithms are sometimes important, but intuition and knowledge is better!
Minimize the number of degrees of freedom that you use
- More degrees of freedom = more complexity.
- A simpler model that explains the same amount of variance is preferred!
- Non-linear trends (e.g. polynomial models) use more degrees of freedom.
- Polynomials are hard to interpret.
7.4 Exercises
Suggested textbook Ch06 exercises: E, I, J, N, P, Q, R, X
- Calculate all ANOVA tables in this lesson using matrix multiplication.
- Explain why Type II SS would not be meaningful for the model \(y_i = \beta_{p-1}x_i^{p-1} + \beta_{p-2}x_i^{p-2} + ... + \beta_2x_i^2 + \beta_1x_i + \beta_0 + \epsilon_i\).
- I performed a Type 3 SS ANOVA for the model \(bodymass_i = \beta_0 + \beta_1flipperlength + \beta_2billlength\). A colleague told me that I should have included \(billdepth\) in this analysis. Will the results from Type 3 SS ANOVA change when I add in this predictor?
- Describe another situation (not polynomial regression) where Type 2 SS ANOVA would be appropriate. Simulate some relevant data and demonstrate.
Solution Hints
In order for Type 2 SS to be appropriate, the predictors need to have a logical order in which to enter the model. Some examples might include a case where researchers have a particular ranking for the predictors in their study, and want to stop adding predictors to the model as soon as they find the first non-significant predictor (I am still struggling to think of context for this).- For the penguins data, fit a model with flipper length, bill length, and bill depth (in that order), and check the output of
anova(). Reverse the order of predictors and repeat. Which values in the ANOVA table stay the same? Which values change? Why do they change? What does this tell you about interpretinganova()output? - Give an example of a context where a collection of predictors might be tested for significance all at once.