8  The Hat Matrix

Author
Affiliation

Dr. Devan Becker

Jam: Residual by Trash.

Published

2024-05-31

8.1 Effect of a Single Point

Leverage and Influence

Show the code 
shiny::runGitHub(repo = "DB7-CourseNotes/TeachingApps", 
    subdir = "Apps/InfluentialPoint")
  • Leverage: affects the line.
    • Measured by the hat matrix.
    • Forcing the line to be what it would be anyway counts as leverage.
  • Influence: affects the line in a “meaningful” way
    • Measured by vibes (and Cook’s Distance).
    • If the point were removed the line would be different.

Leverage \(\ne\) Influence; Extreme Case

Show the code 
# Generate n-1 data points
x <- runif(39, 0, 10)
y <- 4 + 10 * x + rnorm(39, 0, 5)

# Generate nth data point - prefectly on line
x[40] <- 20
y[40] <- 4 + 10 * 20

h <- hatvalues(lm(y ~ x))

plot(x, y)
abline(lm(y ~ x))
text(x[40], y[40], labels = round(h[40], 4),
    adj = c(1,1))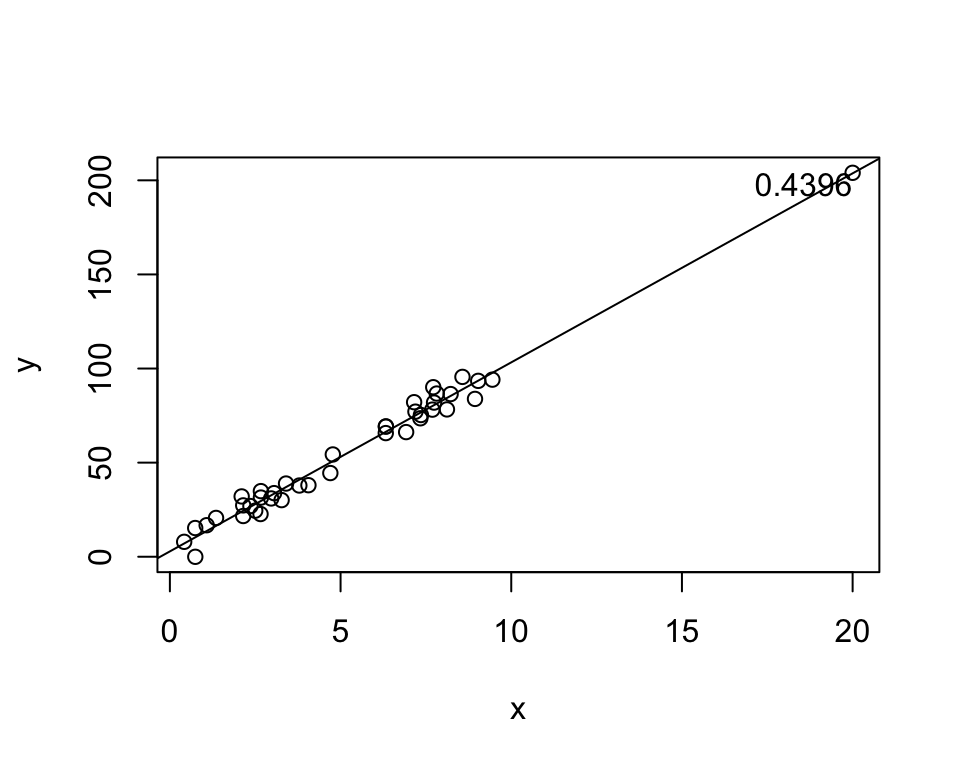

If the point above moves, the entire line moves with it! However, the point happens to be perfectly on the line.

Show the code 
# Generate nth data point - prefectly on line
x[40] <- 20
y[40] <- 50

h <- hatvalues(lm(y ~ x))

plot(x, y)
abline(lm(y ~ x))
text(x[40], y[40], labels = round(h[40], 4),
    adj = c(1,1))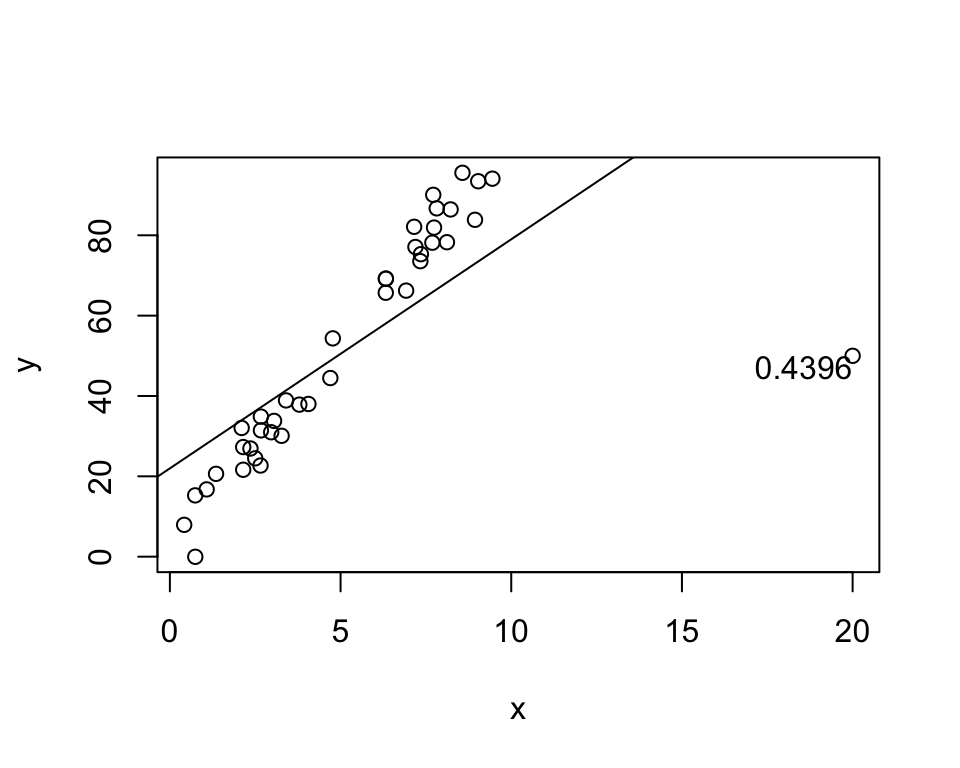

Exact same leverage, but the line is now completely different!

Conclusion: Leverage measures whether the point affects the line, not how.

8.2 Le Chapeau

The Hat Matrix

\[ H = X(X^TX)^{-1}X^T \]

The hat matrix projects \(Y\) onto \(\hat Y\), based on \(X\).

  • \(\hat Y = HY\)
    • \(\hat Y_i = h_{ii} Y_i + \sum_{j\ne i}h_{ij}Y_j\)

In other words, \(h_{ii}\) determines the leverage of the observed point \(y_i\) on it’s own prediction.

Variance-Covariance Matrix of \(\hat{\underline\epsilon}\)

Just like \(\beta_0\) and \(\beta_1\), each sample results in different \(\underline{\hat\epsilon}\).

Across samples, we have: \[ \underline{\hat\epsilon} - E(\underline{\hat\epsilon}) = (I-H)(Y-X\underline{\beta}) = (I-H)\underline{\epsilon} \] and therefore: \[\begin{align*} V(\underline{\hat\epsilon}) &= E([\underline{\hat\epsilon} - E(\underline{\hat\epsilon})][\underline{\hat\epsilon} - E(\underline{\hat\epsilon})]^T)\\ &= [I-H]E(\underline{\epsilon}\underline{\epsilon}^T)[I-H]^T\\ &= [I-H]\sigma^2[I-H]^T\\ &= [I-H]\sigma^2 \end{align*}\] where we used the idempotency and symmetry of \(I-H\).

  • Note: \(h_{ii}\in [0,1]\) for all \(i\), so the variance is positive.

The variance of a residual

Given that \(V(\underline{\hat\epsilon}) = (I-H)\sigma^2\), \[ V(\hat\epsilon_i) = (1-h_{ii})\sigma^2 \]

  • The variance of the residual depends on how much \(Y_i\) effects it’s own estimate.
    • High leverage = low variance.

The correlation between residuals is: \[ \rho_{ij} = \frac{Cov(\hat\epsilon_i, \hat\epsilon_j)}{\sqrt{V(\hat\epsilon_i)V(\hat\epsilon_j)}} = \frac{-h_{ij}}{\sqrt{(1-h_{ii})(1-h_{jj})}} \]

  • Note that \(h_{ij}\in [-1, 1]\). Covariance can be negative or positive.

More H Facts

  1. \(SS(\hat{\underline\beta}) = \hat{\underline\beta}^TX^TY = \hat Y^TY = Y^TH^TY = Y^TH^THY = \hat Y^T\hat Y\)
    • We used the facts \(H^T= H^TH\) and \(\hat Y = HY\).
    • It is super weird that this proof implies \(\hat Y^TY = \hat Y^T\hat Y\), even though \(\hat Y \ne Y\).
  2. \(\sum_{i=1}^nV(\hat Y_i) = trace(H\sigma^2) = p\sigma^2\)
    • \(trace(A)\) is the sum of the diagonal elements of \(A\).
    • \(p\) is the number of parameters.
    • Proof is homework
  3. \(H1 = 1\) if the model contains a \(\beta_0\) term.
    • \(1\) is a column of 1s, not identity matrix.
    • Proof on next slide.
    • \(h_{ii} = 1 - \sum_{j\ne i}h_{ij}\)
      • Note that \(h_{ij}\in[-1, 1]\).

The first one is a little hard to believe! How can \(\hat Y^TY = \hat Y^T\hat Y\) when \(\hat Y \ne Y\)???

First, here’s a demonstration that each equality holds (at least for these particular data):

Show the code 
mylm <- lm(mpg ~ wt, data = mtcars)
X <- model.matrix(mylm)
Y <- mtcars$mpg
Yhat <- predict(mylm)
H <- X %*% solve(t(X) %*% X) %*% t(X)
beta <- as.numeric(coef(mylm))
t(beta) %*% t(X) %*% Y
         [,1]
[1,] 13763.99
Show the code 
t(Yhat) %*% Y
         [,1]
[1,] 13763.99
Show the code 
t(Y) %*% H %*% Y
         [,1]
[1,] 13763.99
Show the code 
t(Y) %*% t(H) %*% H %*% Y
         [,1]
[1,] 13763.99
Show the code 
t(Yhat) %*% Yhat
         [,1]
[1,] 13763.99

Why \(\hat Y^TY = \hat Y^T\hat Y\)? \(\hat Y\) is trying to approximate \(Y\), so you can expect that they’re correlated. If \(Y\) were to be changed so that one of the values were higher, \(\hat Y\) would make a corresponding change. If \(\hat Y\) is too high in one place, it will be too low in another to compensate. This property is not true in general, it’s specifically because of the relationship between \(\hat Y\) and \(Y\) that this works.

Proof that \(H1 = 1\)

Note that \(HX = X\) (as proven on A1).

  1. The first column of \(X\) is all ones (\(\beta_0\) term).
    • \([X]_{i1} = 1\)
  2. Therefore \([HX]_{i1}\) is a column of ones.
    • Every row of \(H\) times the column of 1s in \(X\) results in a column of ones.
  3. \([HX]_{i1}\) is every row of \(H\) times the first column of \(X\).

The first column of \(X\) is 1s, which is equal to the first column of \(HX\), which is \(H\) times a column of ones.

In other words, \(H1 = 1\)

8.3 Studentized Residuals

Internally Studentized (not ideal)

How do you measure the size a residual?

Divide by the variance, of course!

We know that \(V(\hat \epsilon_i) = (1-h_{ii})\sigma^2\), and \[ s^2 = \frac{\sum_{y=1}^n(y_i-\hat y_i)^2}{n-p} = \frac{SSE}{df_E} = MSE \] is an estimate of \(\sigma^2\). Then, \[ r_i = \frac{\hat\epsilon_i}{\sqrt{s^2(1-h_{ii})}} \] is called the internally studentized residual.

“Internally” “Studentized”

Note that \[ s^2 = \frac{\sum_{i=1}^n(y_i-\hat y_i)^2}{n-p} = \frac{\sum_{i=1}^n(\hat\epsilon_i)^2}{n-p} \] and therefore \[ r_i = \frac{\hat\epsilon_i}{\sqrt{s^2(1-h_{ii})}} = \frac{\hat\epsilon_i}{\sqrt{(\hat\epsilon_i^2 + \sum_{j\ne i}\hat\epsilon_j^2)(1-h_{ii})/(n-p)}} \]

  • If \(\hat\epsilon_i\) is large, then \(s^2\) is large.
    • If \(s^2\) is large, then \(r_i\) is small!
    • “Internally”: the variance includes the residual of interest.
  • “Studentized” because “Student” (William Gosset) made it popular.
  • Often called “standardized”.

Externally Studentized Step 1

Like adding/removing predictors and checking the change in SS, we can add/remove points!

  1. Calculate SS
  2. Remove the first point. Estimate the model again and calculate new SS.
  3. Add the first point back, remove the second. Estimate the model again and check the SS.
  4. …

For each point, we have an estimate of the variance without itself.

Externally Studentized Step 2

Skipping the math, \[ s^2_{(i)} = \frac{(n-p)s^2 - \hat\epsilon_i^2/(1-h_{ii})}{n-p-1} \] is the variance of the residuals without observation \(i\).

  • The leverage tells us how much a point changed the model
    • We can see what happened without it
    • No need to re-estimate the model!!!

Let’s demonstrate this quickly!

Show the code 
mylm <- lm(mpg ~ wt, data = mtcars)

# s can be extracted as folows:
s <- summary(mylm)$sigma
# Therefore s1^2 is:
summary(lm(mpg ~ wt, data = mtcars[-1, ]))$sigma^2
[1] 9.409517
Show the code 
# Now let's get it *without* re-fitting the model
# The hat matrix
h <- hatvalues(mylm)
e <- residuals(mylm)
p <- 2
n <- nrow(mtcars)
((n - p) * s^2 - e[1]^2 / (1 - h[1])) / (n - p - 1)
Mazda RX4 
 9.409517

They’re exactly the same, except the second one did not require re-fitting the model! Math is truly astounding.

Externally Studentized Residuals

Use \(s^2_{(i)}\) in place of \(s^2\). \[ t_i = \frac{\hat\epsilon_i}{\sqrt{s_{(i)}^2(1-h_{ii})}} \sim t_{n-p-1} \]

  • Follows a \(t\) distribution!
    • Larger than 2 is suspect, 3 is definitely an outlier!
  • A large \(t_i\) is large relative to the other residuals
  • Usually just called “Studentized”

Most software uses Studentized residuals for plots/diagnostics!

8.4 Cook’s Distance

Better Measures of Influence

The hat matrix is sometimes intepreted as influence, but it has problems.

  • \(y_i\)’s “influence” on it’s own prediction,
    • given all other points.
  • \(0 \le h_{ii} \le 1\)
    • What is a “big” “influence”?
  • How do you explain \(h_{ii}\) to nonstatisticians?

A better measure is how much the predicted value changes with/without the obs.

Cook’s Distance: Change in \(\hat y_i\).

\[ D_i = \frac{\sum_{i=1}^n(\hat y_i - \hat y_{(i)})^2}{ps^2} \]

  • \(\hat y_i\) is the predicted value of \(y_i\) when all data are considered.
  • \(\hat y_{(i)}\) is the predicted value of \(y_i\) when observation \(i\) is removed.
  • \(s^2\) is the MSE of the model with all of the data.
  • \(p\) is the number of parameters
    • \(D_i\) decreases as \(p\) increases!

Again, this would involve re-fitting the model \(n\) times (one re-fit for each observation).

Cook’s Distance: Alternate Form

Again, we can use \(H\) to avoid re-fitting the model.

\[ D_i = \frac{\sum_{i=1}^n(\hat y_i - \hat y_{(i)})^2}{ps^2} = \left[\frac{\hat \epsilon_i}{\sqrt{s^2(1-h_{ii})}}\right]^2\frac{1}{p}\left[\frac{h_{ii}}{1 - h_{ii}}\right] = r_i^2\frac{1}{p}\frac{\text{variance of $i$th predicted value}}{\text{variance of $i$th residual}} \]

  • Cook’s distance is a modification of the internally studentized residual.
    • Variances are based on same “deletion” idea as studentized.
  • Ratio of Variances!
    • \(F\) distribution, mean approaches 1 for large values of \(n\)
      • Cooks Distance of larger than 1 is suspect.

Next Class

Plots!

8.5 Exercises

Suggested Ch08 Exercises: A, C.

  1. In the proof that \(V(\underline{\hat\epsilon_i}) = (1-h_{ii})\sigma^2\), we skipped a few steps. Fill in those steps.
  2. Explain why “a large residual tells us there are small residuals”. It is useful to know that \(\sum_{i=1}^n\hat\epsilon_i = 0\).
  3. Explain where each part of the formula for \(\rho_{ij}\).
  4. Prove that \(\sum_{i=1}^nV(\hat Y_i) = trace(H\sigma^2) = p\sigma^2\). You may use the fact that the “trace” function allows you to move the last term to the front (i.e. you can “cycle” the entries): \(trace(ABCD) = trace(DABC) = trace(CDAB) = trace(BCDA) \ne trace(BACD)\).
  5. For the following data, calculate \(h_{11}\), \(\hat\epsilon_1\), \(s_1\), \(t_1\), and \(D_1\) using R. Plot the data; comment on whether the first value is an outlier, and whether you would know this from each of the calculated values.
Show the code 
set.seed(2112)
x <- c(10, runif(49, 0, 10))
y <- c(50, 2 + 3 * x[-1] + rnorm(49, 0, 3))
mylm <- lm(y ~ x)
X <- model.matrix(mylm)
H <- X %*% solve(t(X) %*% X) %*% t(X)
h11 <- H[1,1]
  1. For the data in the previous question, note that the mean of \(x\) should be around 5. Move the first point to this x-value, keeping the y-value the same. First, make a guess at how do each of \(h_{11}\), \(\hat\epsilon_1\), \(s_1\), \(t_1\), and \(D_1\) change, writing down your guess. Then calculate the values and see if you were right!
  2. The covariance of the estimated residuals is a strange idea to consider. I consider a lot of strange ideas; let’s do this via simulation! Generate a single vector of x values which will be used throughout the simulations, and a preliminary simulation of y values to use for now. For 1000 times, generate new y values, noting the first and second residuals. At the end, find the correlation between these two vectors, and compare to the theoretical correlation found by the \(\rho_{ij}\) formula.
Solution 
x <- runif(40, 0, 10)
y <- 4 + 10 * x + rnorm(40, 0, 10)
X <- cbind(1, x)
H <- X %*% solve(t(X) %*% X) %*% t(X)
cor12 <- -H[1, 2] / sqrt((1 - H[1, 1]) * (1 - H[2, 2]))

R <- 10000
e1 <- c()
e2 <- c()
for (i in 1:R) {
    y <- 4 + 3 * x + rnorm(40, 0, 3)
    e <- residuals(lm(y ~ x))
    e1[i] <- e[1]
    e2[i] <- e[2]
}
cor(e1, e2)
[1] 0.01971098
cor12
[1] 0.006790357

It’s a simulation and there’s a lot of variance, but I’m satisfied with that.

The important thing: The correlation of residuals is based on if we were to do many different samples (with the x-values the same each time).