Appendix E — Hat Matrix and Residuals in R

Author
Affiliation

Dr. Devan Becker

Wilfrid Laurier University

Published

2024-05-29

The Hat Matrix

\[ H = X(X^TX)^{-1}X^T \]

In R, we can calculate the diagonal of the hat matrix as follows:

Show the code 
mylm <- lm(mpg ~ disp + wt, data = mtcars)
hatvalues(mylm) |> unname()
 [1] 0.04339369 0.04550894 0.06309504 0.03877647 0.14078260 0.04406584
 [7] 0.11516157 0.09635365 0.09875274 0.11012510 0.11012510 0.08141444
[13] 0.04168379 0.04521644 0.17206264 0.19889125 0.19275897 0.08015728
[19] 0.12405357 0.09579747 0.05703451 0.06246825 0.05648077 0.06838477
[25] 0.14119998 0.08720679 0.07149742 0.16032953 0.18794989 0.05044456
[31] 0.04474121 0.07408572

Extracting the Diagonals from H

There isn’t a built-in function for the full hat matrix (the diagonals are usually all you’ll need). For demonstration, here are some demonstrations of the features of the hat matrix.

Show the code 
X <- model.matrix(mylm)
H <- X %*% solve(t(X) %*% X) %*% t(X)
all.equal(diag(H), hatvalues(mylm))
[1] TRUE

Features of H

In the code below, I use the unname() function because mtcars has rownames which make the output harder to see (this used to be the norm in R, but it’s fallen out of fashion).

Show the code 
colSums(H) |> unname()
 [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Show the code 
rowSums(H) |> unname()
 [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Show the code 
range(H) # -1 <= h_{ij} <= 1
[1] -0.1076609  0.1988913
Show the code 
range(diag(H)) # 0 <= h_{ii} <= 1
[1] 0.03877647 0.19889125
Show the code 
H %*% rep(1, ncol(H)) # H1 = 1
                    [,1]
Mazda RX4              1
Mazda RX4 Wag          1
Datsun 710             1
Hornet 4 Drive         1
Hornet Sportabout      1
Valiant                1
Duster 360             1
Merc 240D              1
Merc 230               1
Merc 280               1
Merc 280C              1
Merc 450SE             1
Merc 450SL             1
Merc 450SLC            1
Cadillac Fleetwood     1
Lincoln Continental    1
Chrysler Imperial      1
Fiat 128               1
Honda Civic            1
Toyota Corolla         1
Toyota Corona          1
Dodge Challenger       1
AMC Javelin            1
Camaro Z28             1
Pontiac Firebird       1
Fiat X1-9              1
Porsche 914-2          1
Lotus Europa           1
Ford Pantera L         1
Ferrari Dino           1
Maserati Bora          1
Volvo 142E             1

Extracting the residuals

See ?influence.measures.

Show the code 
?rstandard
cooks.distance(mylm)

The broom package

The broom package has a wonderful function called augment(). This function sets up our data so that it’s super easy to see what we need.

Show the code 
library(broom)
augment(mylm)
# A tibble: 32 × 10
   .rownames     mpg  disp    wt .fitted .resid   .hat .sigma .cooksd .std.resid
   <chr>       <dbl> <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>      <dbl>
 1 Mazda RX4    21    160   2.62    23.3 -2.35  0.0434   2.93 0.0102      -0.822
 2 Mazda RX4 …  21    160   2.88    22.5 -1.49  0.0455   2.95 0.00435     -0.523
 3 Datsun 710   22.8  108   2.32    25.3 -2.47  0.0631   2.93 0.0172      -0.876
 4 Hornet 4 D…  21.4  258   3.22    19.6  1.79  0.0388   2.95 0.00524      0.624
 5 Hornet Spo…  18.7  360   3.44    17.1  1.65  0.141    2.95 0.0203       0.609
 6 Valiant      18.1  225   3.46    19.4 -1.28  0.0441   2.96 0.00309     -0.448
 7 Duster 360   14.3  360   3.57    16.6 -2.32  0.115    2.93 0.0309      -0.845
 8 Merc 240D    24.4  147.  3.19    21.7  2.73  0.0964   2.92 0.0344       0.984
 9 Merc 230     22.8  141.  3.15    21.9  0.890 0.0988   2.96 0.00378      0.322
10 Merc 280     19.2  168.  3.44    20.5 -1.26  0.110    2.96 0.00869     -0.459
# ℹ 22 more rows

Notice that it includes:

  • .fitted = \(X\underline{\hat\beta} = \hat Y\)
  • .resid = \(\hat{\underline\epsilon}\)
  • .hat = \(diag(H)\)
  • .sigma = \(s_{(i)}\)
  • .cooksd = D
  • .std.resid = are these standardized or studentized residuals? Find out yourself as homework!!

Plotting the residuals

If you’ve ever accidentally typed plot(mylm), you’ve seen some plots of the residuals.

Show the code 
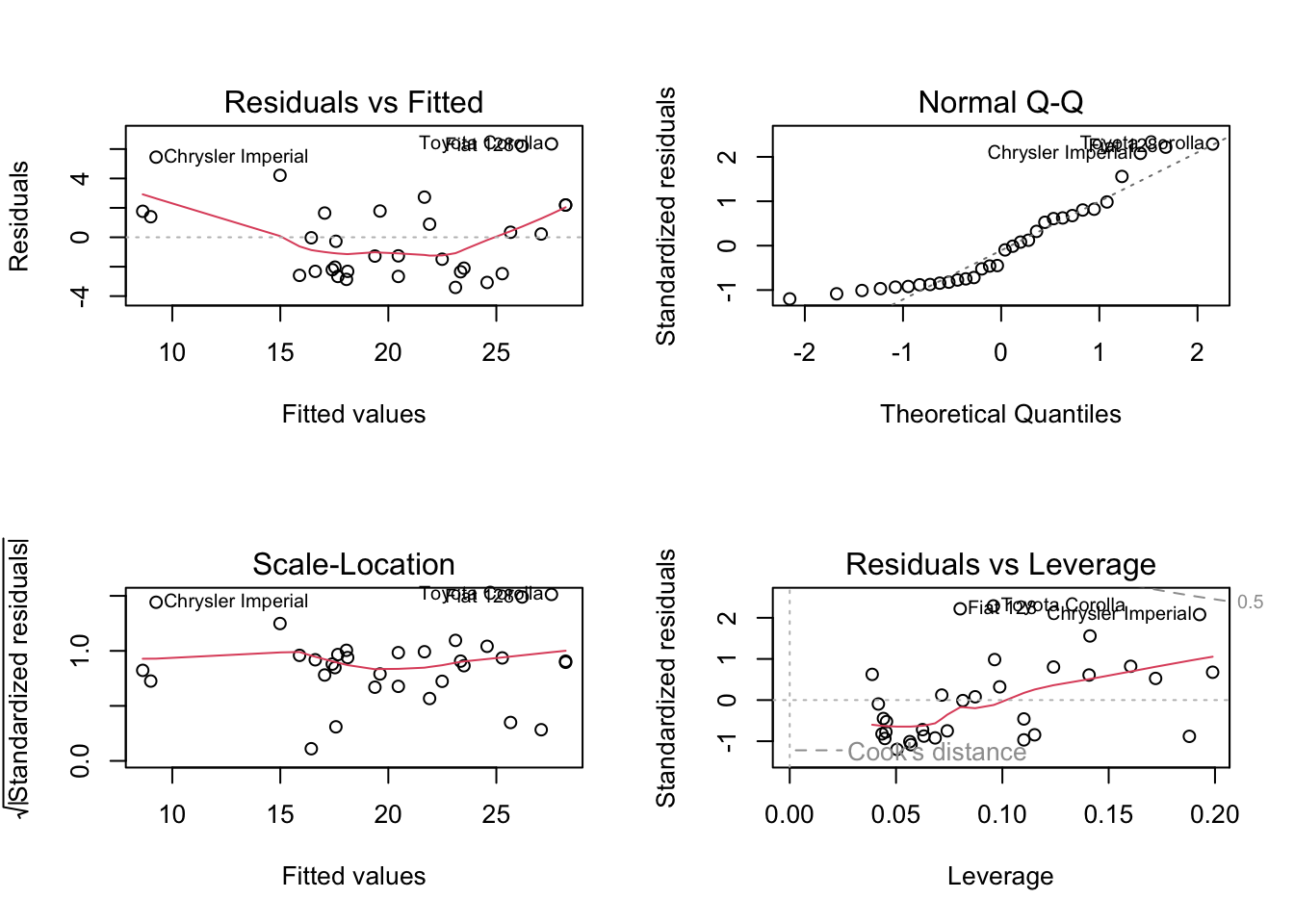
par(mfrow = c(2, 2)) # plot.lm produces four plots.
plot(mylm) # ?plot.lm

You can access individual plots with the which argument.

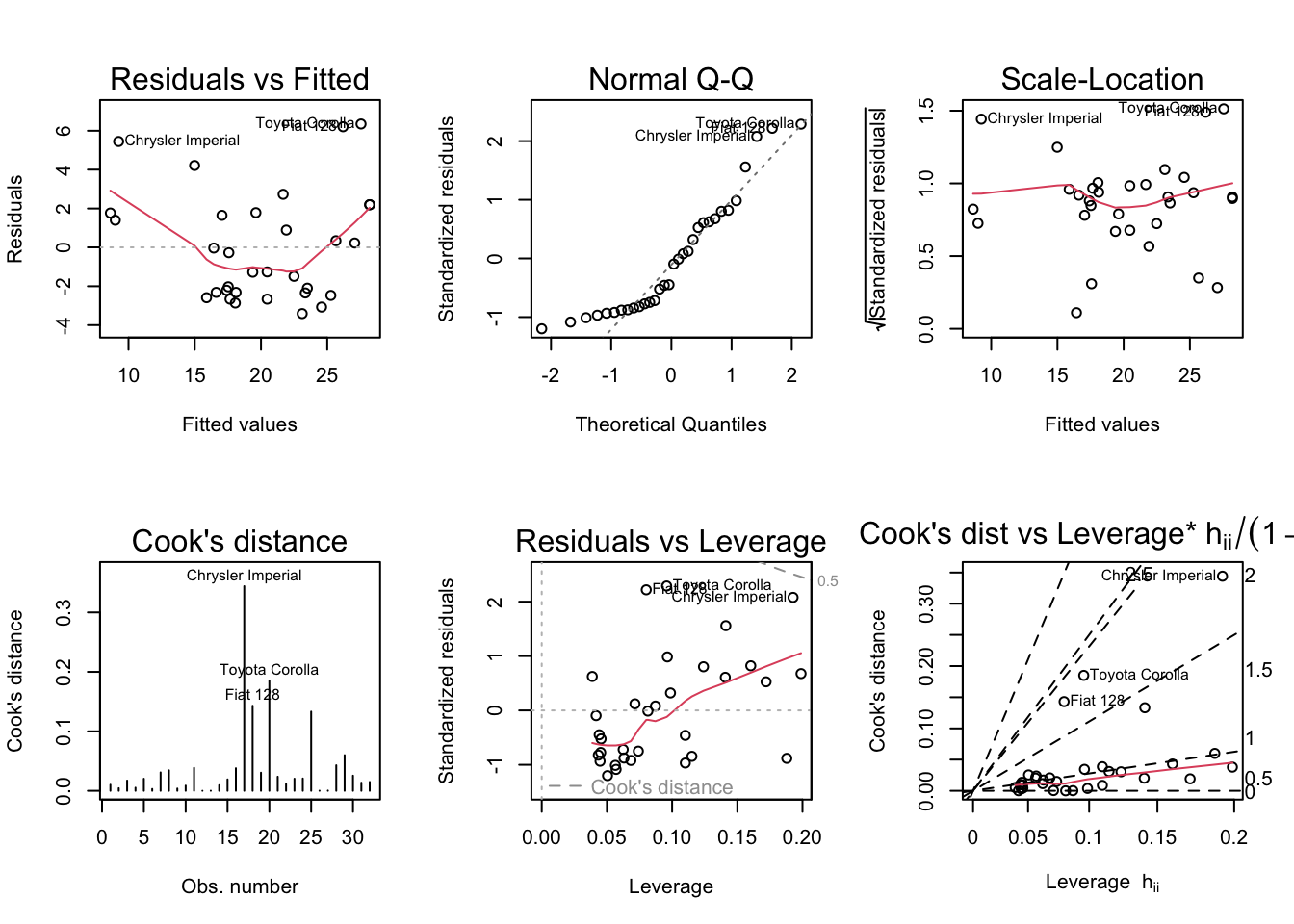
Show the code 
par(mfrow = c(2, 3))
plot(mylm, which = 1:6)

99% of the time, the default plots are the ones you’ll want to look at. For teaching purposes, we’ll look at the extra.

Demonstrations

We’ll use the Ozone data from the mlbench package.

  • V4 is response (measurement of Ozone)
  • V5 is atmospheric pressure
  • V6 is wind speed
  • V7 is humidity
  • We’ll ignore the rest.
Show the code 
library(mlbench)
data(Ozone)
str(Ozone) # V4 is response (measurement of Ozone)
'data.frame':   366 obs. of  13 variables:
 $ V1 : Factor w/ 12 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ V2 : Factor w/ 31 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
 $ V3 : Factor w/ 7 levels "1","2","3","4",..: 4 5 6 7 1 2 3 4 5 6 ...
 $ V4 : num  3 3 3 5 5 6 4 4 6 7 ...
 $ V5 : num  5480 5660 5710 5700 5760 5720 5790 5790 5700 5700 ...
 $ V6 : num  8 6 4 3 3 4 6 3 3 3 ...
 $ V7 : num  20 NA 28 37 51 69 19 25 73 59 ...
 $ V8 : num  NA 38 40 45 54 35 45 55 41 44 ...
 $ V9 : num  NA NA NA NA 45.3 ...
 $ V10: num  5000 NA 2693 590 1450 ...
 $ V11: num  -15 -14 -25 -24 25 15 -33 -28 23 -2 ...
 $ V12: num  30.6 NA 47.7 55 57 ...
 $ V13: num  200 300 250 100 60 60 100 250 120 120 ...
Show the code 
Ozone <- Ozone[complete.cases(Ozone), ]

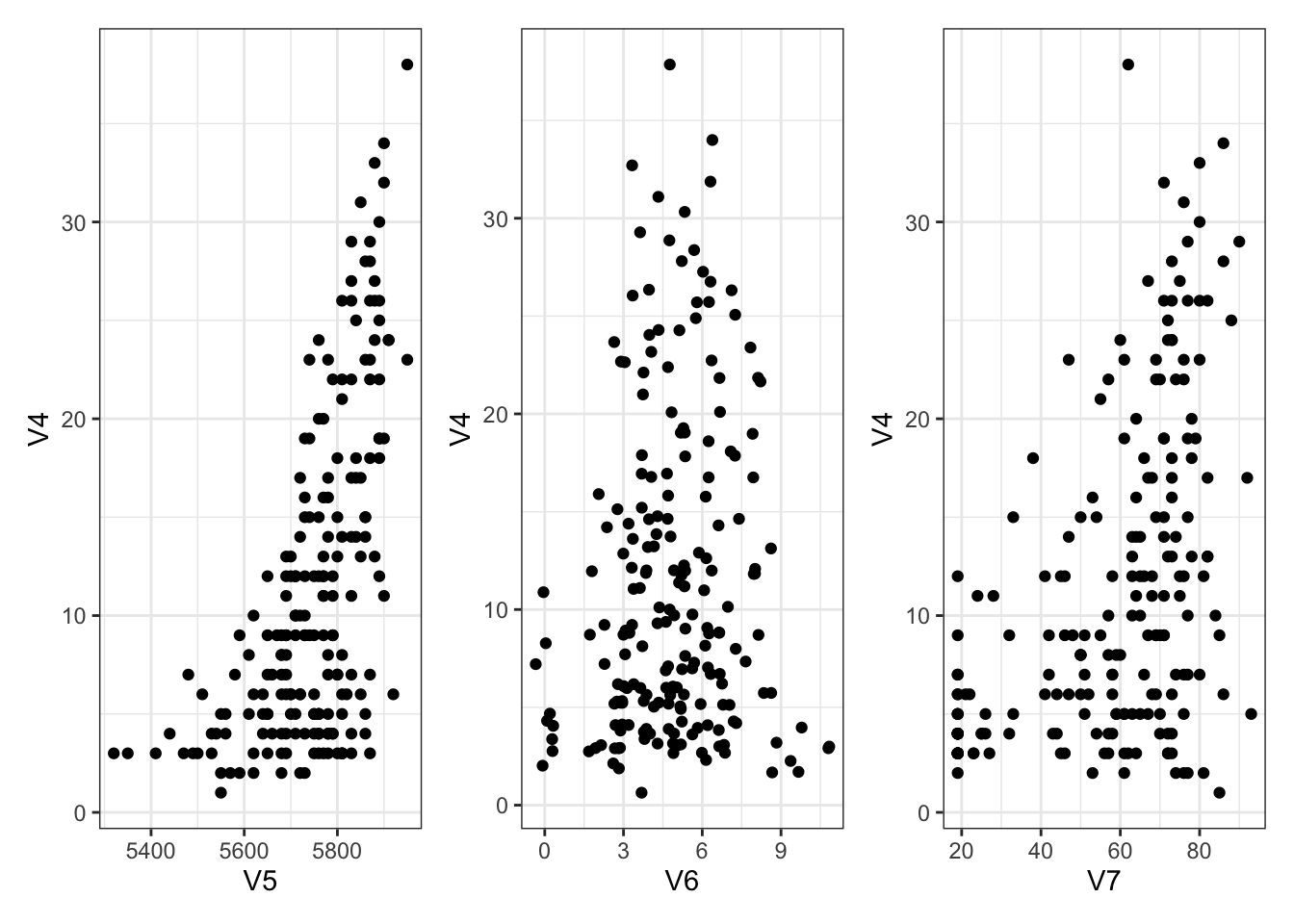
A small amount of exploration first:

Show the code 
library(ggplot2)
theme_set(theme_bw())
library(patchwork)
g5 <- ggplot(Ozone) +
    aes(x = V5, y = V4) +
    geom_point()
g6 <- ggplot(Ozone) +
    aes(x = V6, y = V4) +
    geom_jitter() # deal with overlapping points
g7 <- ggplot(Ozone) +
    aes(x = V7, y = V4) +
    geom_point()
g5 + g6 + g7

Now let’s check some residuals!

  • Change .resid to .std.resid.
    • Try rstudent(olm) as well.
  • Change .hat to .cooksd.
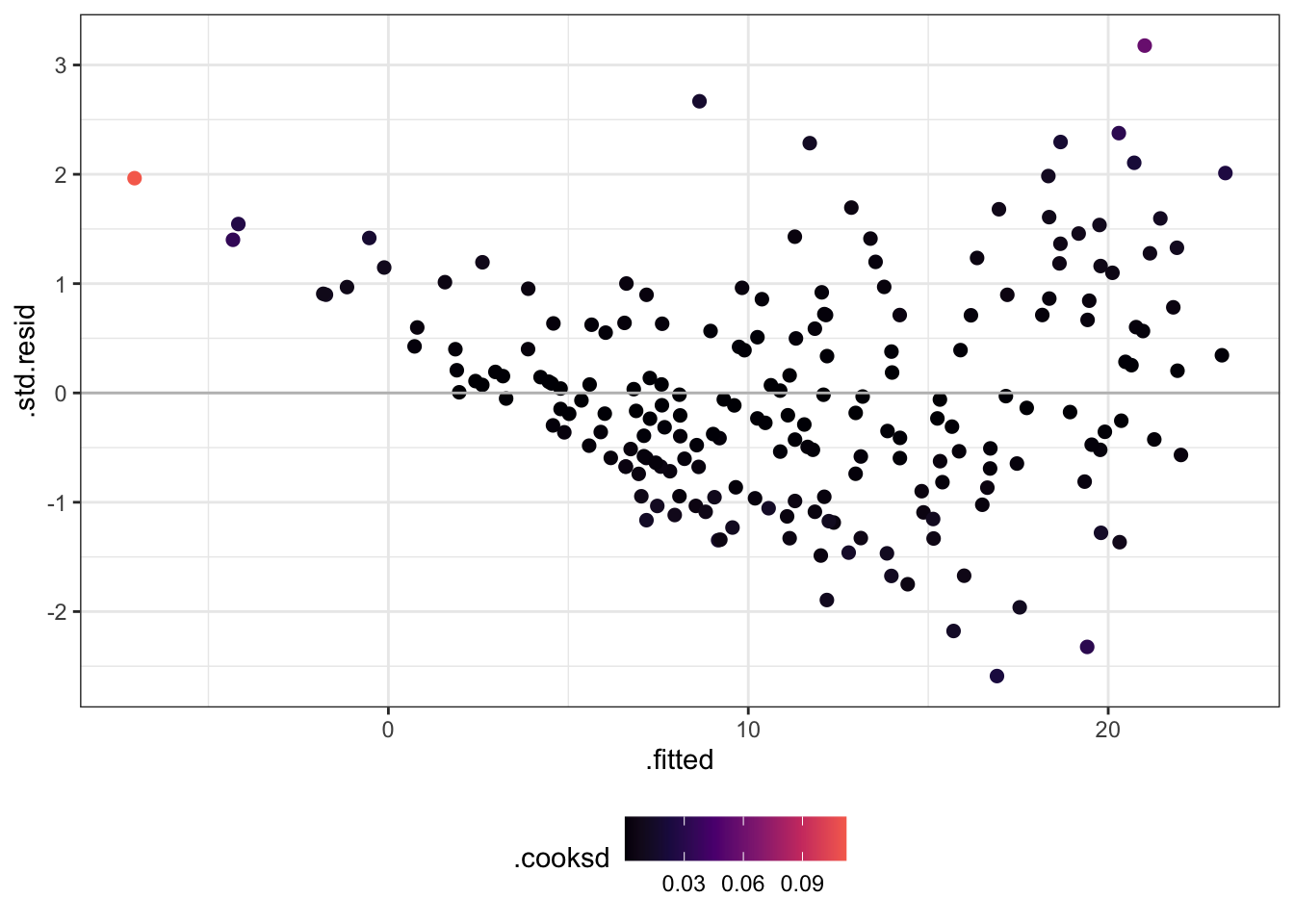
Show the code 
library(dplyr)
olm <- lm(V4 ~ V5 + V6 + V7, data = Ozone)
augment(olm) %>%
    ggplot() +
        aes(x = .fitted, y = .std.resid, col = .cooksd) +
        scale_colour_viridis_c(option = 2, end = 0.7) +
        theme(legend.position = "bottom") +
        geom_point(size = 2) +
        geom_hline(yintercept = 0, colour = "grey")

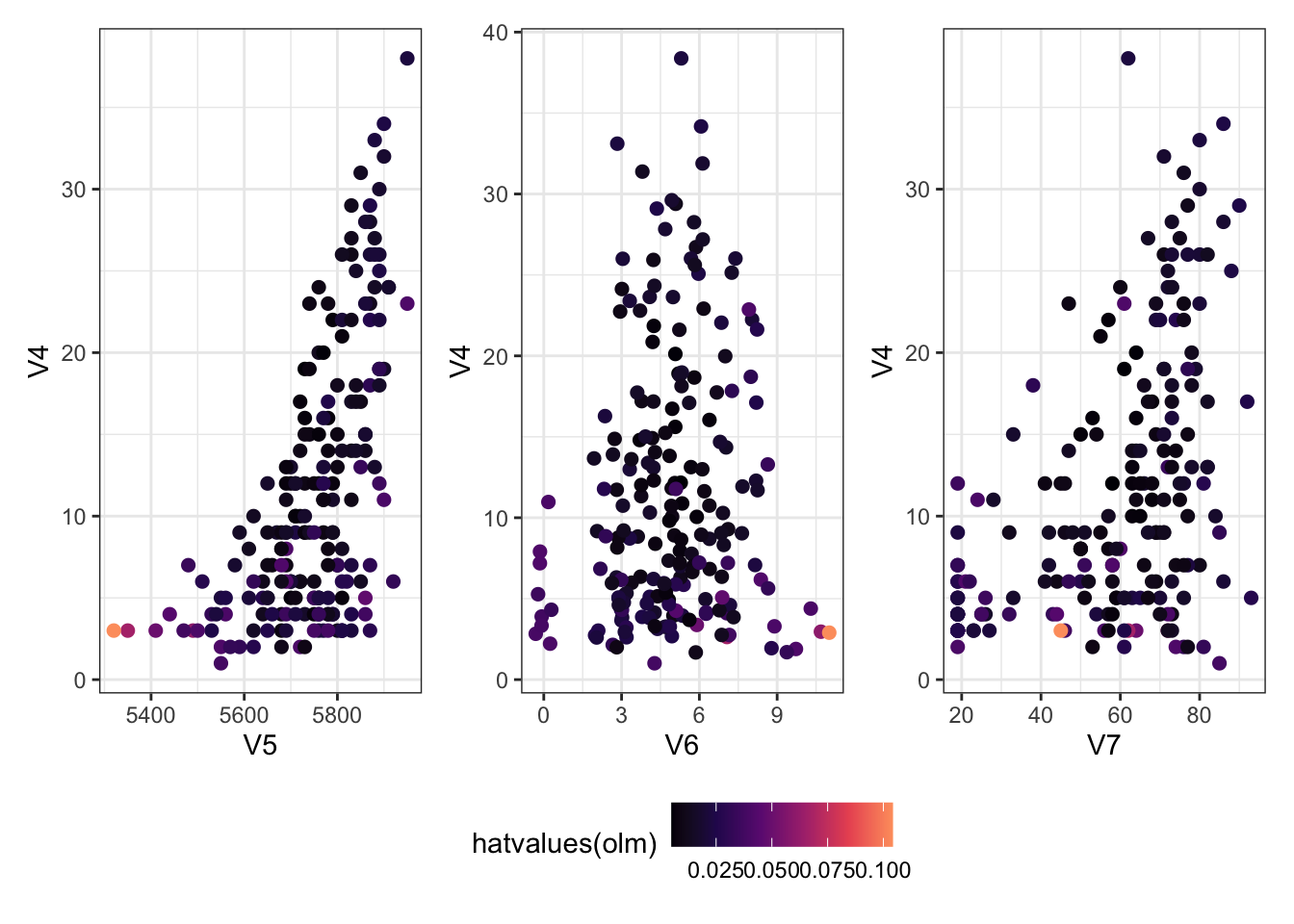
Which ones have a large hat value?

The plots below are the same as the ones above, but coloured according to the hat values.

Show the code 
g5 <- ggplot(Ozone) +
    aes(x = V5, y = V4, col = hatvalues(olm)) +
    geom_point(size = 2)
g6 <- ggplot(Ozone) +
    aes(x = V6, y = V4, col = hatvalues(olm)) +
    geom_jitter(size = 2) # deal with overlapping points
g7 <- ggplot(Ozone) +
    aes(x = V7, y = V4, col = hatvalues(olm)) +
    geom_point(size = 2)
(g5 + g6 + g7) +
    plot_layout(guides = "collect") &
    scale_colour_viridis_c(option = 2, end = 0.8) &
    theme(legend.position = "bottom")

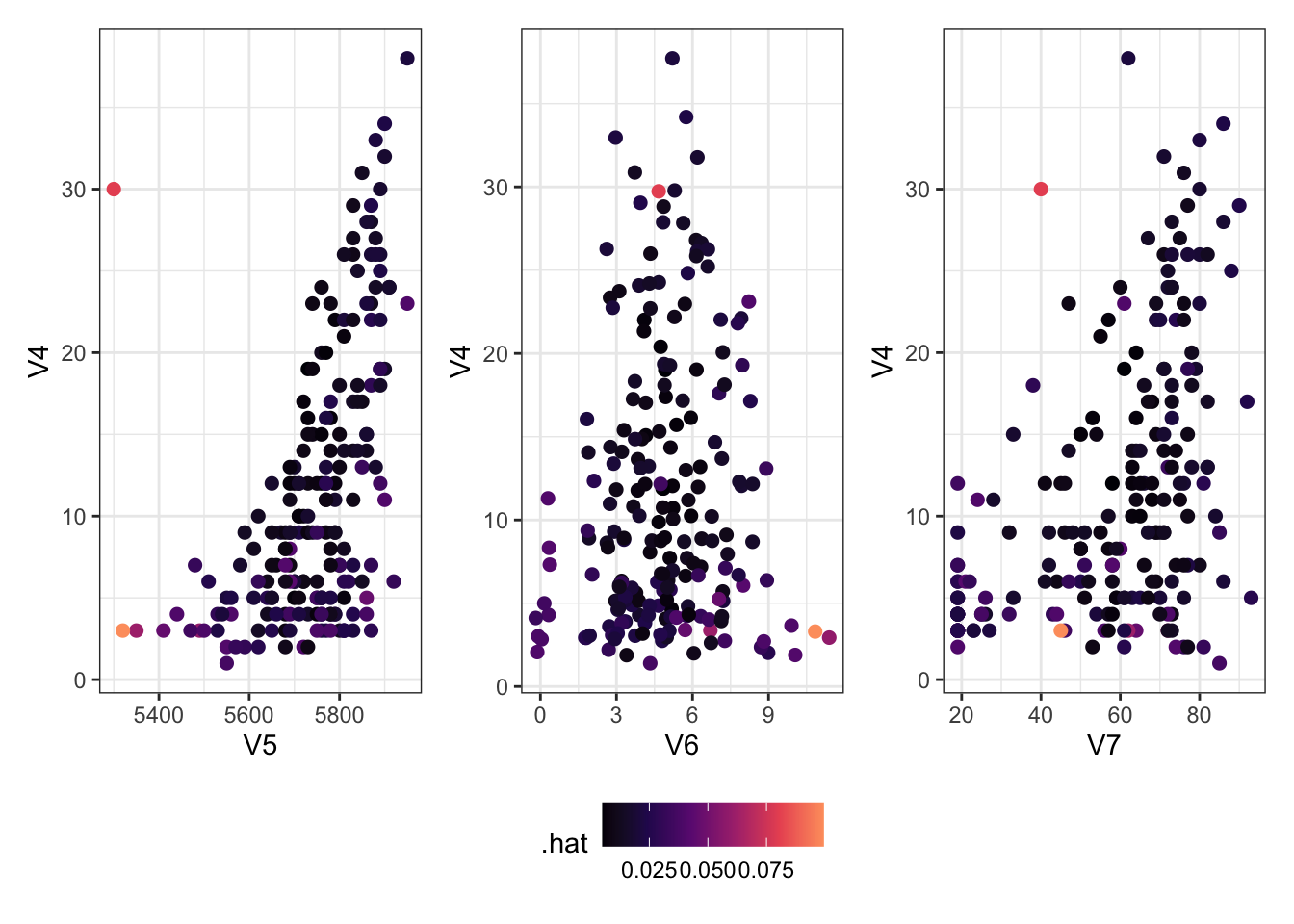
Adding an Outlier

Let’s add an outlier to see what happens with these data.

Show the code 
newzone <- Ozone[, c(4:7)]
newzone <- rbind(newzone,
    data.frame(V4 = 30, V5 = 5300, V6 = 5, V7 = 40))
newlm <- augment(lm(V4 ~ ., data = newzone))

g5 <- ggplot(newlm) +
    aes(x = V5, y = V4, col = .hat) +
    geom_point(size = 2)
g6 <- ggplot(newlm) +
    aes(x = V6, y = V4, col = .hat) +
    geom_jitter(size = 2) # deal with overlapping points
g7 <- ggplot(newlm) +
    aes(x = V7, y = V4, col = .hat) +
    geom_point(size = 2)
(g5 + g6 + g7) +
    plot_layout(guides = "collect") &
    scale_colour_viridis_c(option = 2, end = 0.8) &
    theme(legend.position = "bottom")

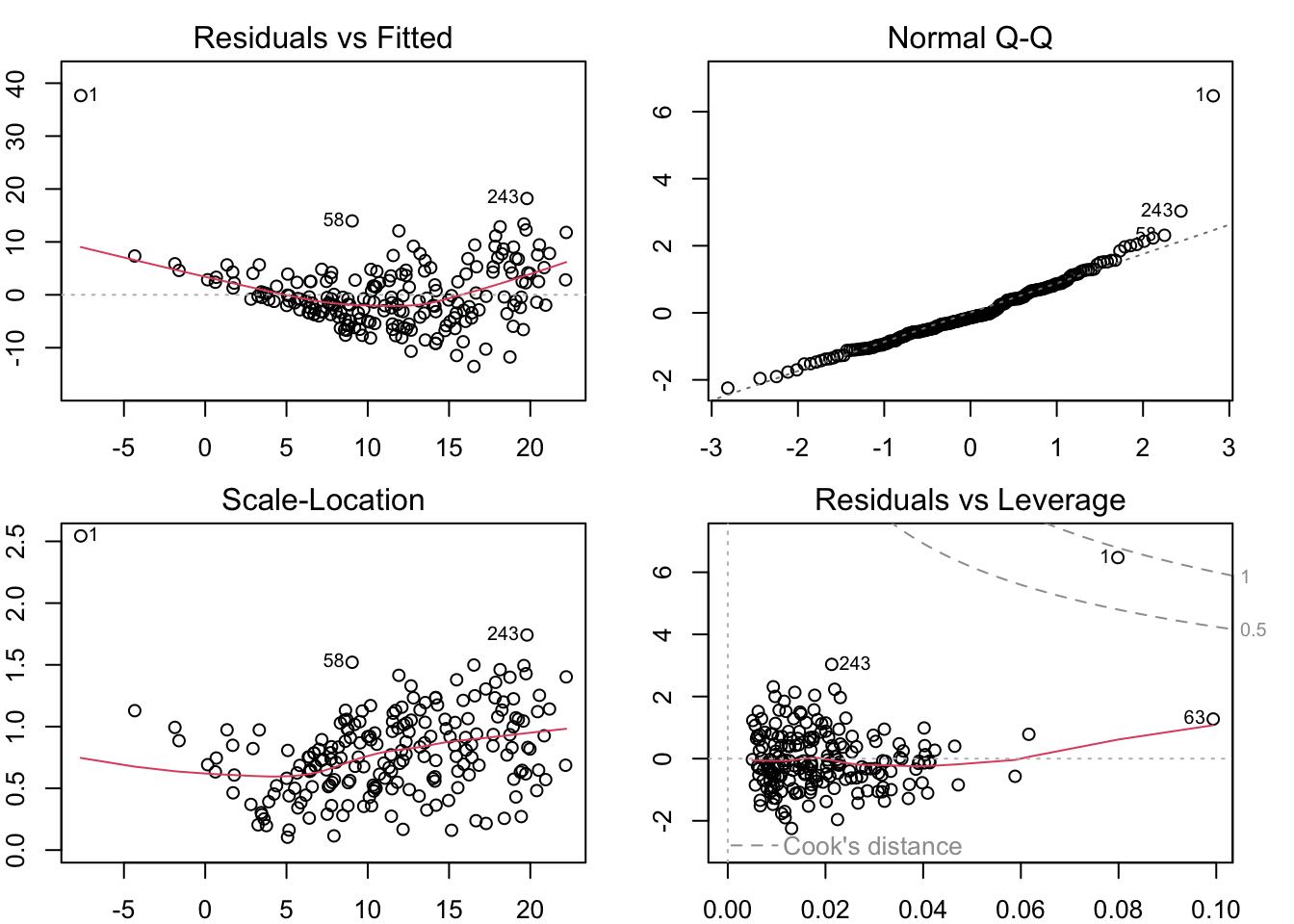
Using R’s Built-In Diagnostics

Show the code 
par(mfrow = c(2, 2), mar = rep(2, 4))
plot(lm(V4 ~ ., data = newzone))

Show the code 
newzone[row.names(newzone) %in% c(1, 58, 243), ]
    V4   V5 V6 V7
58  23 5740  3 47
243 38 5950  5 62
1   30 5300  5 40
  1. Huge residual!
    • This plot also just has a bad pattern
  2. Deviates from normality!
    • Otherwise this looks pretty good.
  3. Large standardized residual
    • Clear pattern without the outlier
  4. Cook’s distance is massive compared to the others
    • Potentially some large \(D_i\)’s
  5. In the corner
    • Otherwise this looks okay-ish
  6. Last plot also shows it as something different (harder to interpret)

What to do with a large residual?

  • Misrecorded: remove or fix, if possible
    • Fires with negative lengths (MDY versus DMY)
    • CO2 measured as -99 (code for NA in a system with no NA option)
    • Heights measured in the wrong units
  • Real, but large residual: Consider whether it’s actually part of the population of interest
    • Studying heights and got a basketball player in your sample? That’s a real data point and your model should allow for it!
    • Studying fish and a shark was included? That’s real, but maybe you should narrow your scope!
  • Many large outliers: you may need to try more predictors or a non-linear model.

DO NOT remove a point simply because it’s an outlier!!!